介绍
我们经常从天气预报中听到:明天的降水率是80%。这意味着什么?我们很难直白地解释这种说法,尤其是从概率学派的角度:无限次(或非多次)地重复下雨/不下雨实验是不现实的。
贝叶斯方法可以解释这种说法。以下句子摘自《为黑客设计的概率规划与贝叶斯方法》一书,它完美地总结了贝叶斯学派的关键思想之一。
贝叶斯世界观将概率解释为事件可信度的量度,即我们对事件发生有多少信心。
这意味着在贝叶斯方法中,我们永远不能绝对确定自己的“信念”,但可以肯定表达我们对于相关事件发生有多少信心。此外随着收集到更多数据,我们可以对自己的信念更加信心。
作为一名科学家,我被训练着去相信数据,并且对所有事物都很谨慎。所以我认为贝叶斯推理是相当直观的。
但是使用贝叶斯推断在计算和概念上通常具有挑战性。完成工作经常需要大量耗时而复杂的数学计算。即使作为数学家,我有时也觉得这些计算很乏味;特别是要快速了解待解决的问题时。
幸运的是我的导师AustinRochford最近向我介绍了一个名为PyMC3的程序包,它使我们能够进行数值贝叶斯推理。本文将通过一个具体示例快速介绍PyMC3。
一个具体的例子
假设我们有一枚硬币,我们将其翻转三遍,结果是:
[0,1,1]
其中0表示硬币背面向上,1表示人头向上。我们有信心说这是一个公平的硬币吗?换句话说,如果让θ为人头向上的概率,那么证据是否足以支持θ= 0.5的说法?
由于除了上述实验的结果外,我们对硬币一无所知,因此很难确定地说什么。从概率学派的角度来看,θ的点估计为:
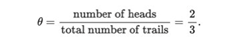
尽管这个数字是合理的,但是概率学派的方法并不能真正为它提供一定的信心置信。特别是如果我们进行更多试验,则可能会得到不同的θ点估计。
这是贝叶斯方法可以提供一些改进的地方。这个想法很简单,因为我们对θ一无所知,因此可以假设θ可以是[0,1]上的任何值。在数学上,我们的先验信念是θ遵循均匀分布Uniform(0,1)分布。悄悄提醒需要复习数学的同学,Uniform(0,1)的pdf如下:
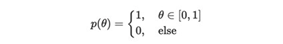
然后我们可以使用证据/观察来更新我们关于θ分布的信念。
让我们正式将D称为证据(我们的例子中是抛硬币的结果。)根据贝叶斯规则,后验分布可通过以下公式计算:
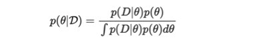
其中p(D |θ)是似然函数,p(θ)是先验分布(在这种情况下,为Uniform(0,1))从这里开始有两种方法。
显式方法
在这个特定示例中,我们可以手动完成所有操作。更准确地说,给定θ三个抛硬币中有2个人头向上的概率为:
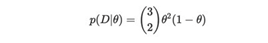
通过假设,p(θ)= 1。接下来,我们计算分母:
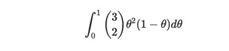
通过一些简单计算,我们可以看到上述积分等于1/4,因此:
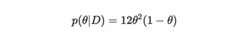
注意:通过相同的计算,我们还可以看到,如果θ的先验分布是参数为α,β的Beta分布,即p(θ)= B(α,β),并且样本大小为N,k它们是人头向上的次数,则θ的后验分布由B(α+ k,β+ N-K)给出。在我们的案例下,α=β= 1,N = 3,k = 2。
量化方法
在显式方法中,我们能够使用共轭先验来显式计算θ的后验分布。但有时使用共轭先验来简化计算,它们可能无法反映现实。此外找到共轭先验并不总是可行的。
我们可以通过使用马尔可夫链蒙特卡洛(MCMC)方法来近似后验分布来克服此问题。这里的数学计算很多,但是出于本文目的,我们不会深入探讨。我们将侧重解释如何使用PyMC3实现此方法。
运行代码前,我们导入以下软件包。
import pymc3 as pm
import scipy.stats as stats
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
from IPython.core.pylabtools import figsize
首先我们需要初始化θ的先验分布。在PyMC3中,可以通过以下代码来实现。
with pm.Model() as model:
theta=pm.Uniform('theta',lower=0, upper=1)
然后我们将模型与观测数据拟合。这可以通过以下代码完成。
occurrences=np.array([1,1,0]) #our observation
with model:
obs=pm.Bernoulli("obs", p,observed=occurrences) #input the observations
step=pm.Metropolis()
trace=pm.sample(18000, step=step)
burned_trace=trace[1000:]
在内部计算逻辑上,PyMC3使用Metropolis-Hastings算法来近似后验分布。Trace功能确定从后验分布中抽取的样本数。最后由于该算法在开始时可能不稳定,因此在经过一定的迭代周期后,提取的样本更有用。这就是我们代码最后一行的目的。
然后,我们可以绘制从后验分布获得的样本的直方图,并将其与真实密度函数进行比较。
from IPython.core.pylabtools import figsize
p_true=0.5
figsize(12.5, 4)
plt.title(r"Posterior distribution of$\theta$")
plt.vlines(p_true,0, 2, linestyle='--',label=r"true $\theta$ (unknown)", color='red')
plt.hist(burned_trace["theta"],bins=25, histtype='stepfilled', density=True, color='#348ABD')
x=np.arange(0,1.04,0.04)
plt.plot(x, 12*x*x*(1-x), color='black')
plt.legend()
plt.show()
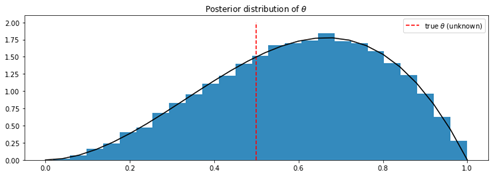
我们可以清楚地看到,数值逼近非常接近真实的后验分布。
如果我们增加样本容量?
如前所述,获得的数据越多,我们对θ的真实值的信心就越大。让我们通过一个简单的模拟来检验我们的假设。
我们将随机抛硬币1000次,使用PyMC3估算θ的后验分布。然后绘制从该分布获得样本的直方图。所有这些步骤都可以通过以下代码来完成:
N=1000 #the number of samples
occurences=np.random.binomial(1, p=0.5, size=N)
k=occurences.sum() #the number of head
#fit the observed data
with pm.Model() as model1:
theta=pm.Uniform('theta', lower=0,upper=1)
with model1:
obs=pm.Bernoulli("obs",theta, observed=occurrences)
step=pm.Metropolis()
trace=pm.sample(18000, step=step)
burned_trace1=trace[1000:]
#plot the posterior distribution of theta.
p_true=0.5
figsize(12.5, 4)
plt.title(r"Posterior distribution of $\theta for sample sizeN=1000$")
plt.vlines(p_true,0, 25, linestyle='--', label="true $\theta$(unknown)", color='red')
plt.hist(burned_trace1["theta"], bins=25, histtype='stepfilled',density=True, color='#348ABD')
plt.legend()
plt.show()
下图为我们得到的结果:
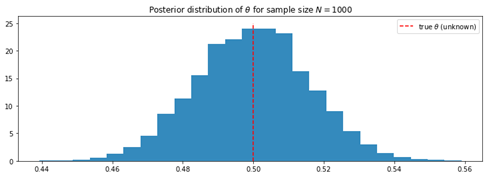
如图所示,后验分布现在以θ的真实值为中心。
我们可以通过取样本均值来估算θ。
burned_trace1['theta'].mean()
0.4997847718651745
这确实接近真实答案。
结论
PyMC3可以很好地执行统计推断任务,它使概率编程变得相当轻松。
参考资料:
[1] https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers
原文标题:
Introduction to PyMC3: A Python package forprobabilistic programming
原文链接:
https://towardsdatascience.com/introduction-to-pymc3-a-python-package-for-probabilistic-programming-5299278b428
*博客内容为网友个人发布,仅代表博主个人观点,如有侵权请联系工作人员删除。