在开始之前，我们需要预习一下二项分布。

还是丢硬币的例子，丢某块特制的硬币，假设正面向上的概率是P，则掷出图片次，有K次向上的概率P是多少？

将硬币正面朝上的次数记为随机变量X，则有

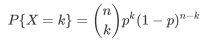
这种分布就是二项分布。容易证明，二项分布的数学期望 E(X)=np

泊松分布

我们回到泊松分布。先来看一个生活场景。

宋朝庆历年间，刘姥姥由于生活压力，不得不根据祖传秘方发明总结并始创了一种名叫十二香的调料，并开始在市场上叫卖。刘姥姥在街上卖了半年，由于本小利薄，味道赞绝，一直供不应求，但由于制作周期长，原料准备流程复杂，而且保存时间较短，一直无法提高产量。

这一天，刘姥姥终于决定要弄清楚她每天刚制作的调料究竟是如何被火速买光的，以便提高进货量来增加销量。

刘姥姥首先买了绝对充足的原料，熬夜制作了足份的十二香。卖了一周，每天开张五个时辰，结果没卖光剩下的调料全部变质了只能丢掉，心疼的她难受了小半天。不过她总算是记录下了宝贵的数据：这七天内每天调料的销售情况。

刘姥姥看着这用浪费的调料换来的宝贵数据，想了想，打算以后每天都按照日出货平均数：即10份来进原材料，制作，保存。

刘姥姥的儿子刘大耳不同意。他认为：如果按照10份准备，那七天里有四天都不够卖的，这可能会使王县令的老婆买不到调料，将来一定会闹事。

刘大耳说：我们应该保证有90%以上的把握准备最少的调料每日的份数，使来咱这购买十二香的客人需求全都满足。我们可以如此如此，这般这般……

于是刘姥姥就听从了大耳儿的建议，从此之后，生意更加兴隆，至于王县令后来入伙加盟，生意不断做大，后来更是推陈出新创立了十三香举世闻名，当然这都是后话了。

那么当时刘大耳的方案是什么呢？接下来将一一道来。

刘姥姥每天卖五个时辰，也就是600分钟，如果每分钟最多只能卖出一份调料，且在这一分钟卖出调料的概率是P，那么这一天卖出10份调料的概率可以通过二项分布计算：

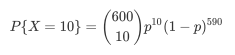
但是王县令家里人丁兴旺，他老婆有时候会一次买几十份调料，那每分钟可能就卖出去不止一份调料。于是刘大耳将分割六个时辰的时间间隔进一步缩小，分割成图片，再利用极限的思想：

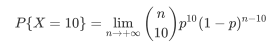
再抽象一些，那么在某天能卖出图片份调料的概率应该是：

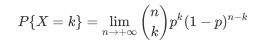
那么P如何计算呢？还记得二项分布的期望吗：假设

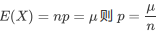
而我们可以使用当图片比较小的时候计算平均值得到的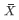来近似。

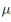另外，需要注意的是，在如上假设下，当n越来越大时，p值也会越来越小。

我们来进一步计算一下这个概率：

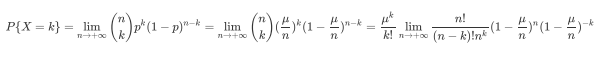
而容易看出：

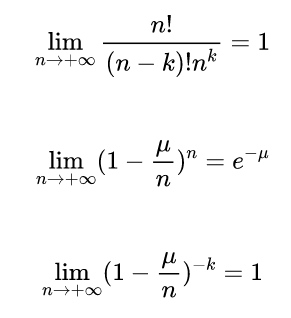
因此我们得到：

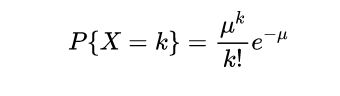
至此，我们就得到了教科书中泊松分布的概率密度函数！

刘大耳用图片近似替代这里的图片。于是我们可以利用python中的scipy库快速画出刘姥姥每天卖出图片份十二香的概率密度曲线和累计分布函数。

import numpy as np

from scipy import stats

from matplotlib import pyplot as plt

mu = 10

x = np.arange(0,101,1) 

plist = stats.poisson.pmf(x,mu) 

clist = stats.poisson.cdf(x,mu)

plt.plot(x,plist,label='poisson distribution pmf') # 

plt.plot(x,cdflist,label='poisson distribution cdf') 

plt.xlim((-1,15))

plt.grid() 

plt.legend() 

plt.title(r'Poisson Distribution $\mu$:10') 

plt.show()

如图1。近似从图中得出：每天准备14份十二香，就有超过90%的把握不让顾客乘兴而来空手而去。

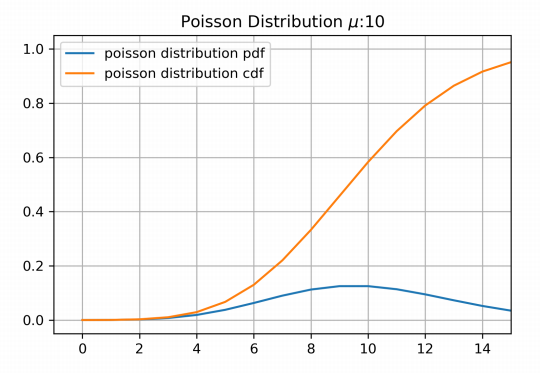
从上面的例子可以看出，泊松分布可以近似模拟一个离散事件在连续时间内发生的次数的概率分布。真实世界中有很多场景都和泊松分布有关，比如某网站在某段时间内的点击率；客服中心在某段时间内接到电话的次数；医院在某段时间内接生的婴儿；放射性元素在某段时间内衰变的粒子个数……

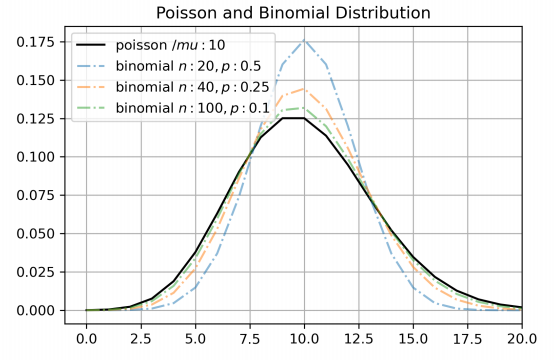
事实上我们通过上面的推导过程也能看出：当p很小（或n很大）时的二项分布就近似等于泊松分布，此时我们也可以用泊松分布来快速近似计算起来更麻烦的二项分布。不信的话我们把代码和图撂在这，请看图2。

import numpy as np 

from scipy import stats 

from matplotlib import pyplot as plt

mu = 10 

x = np.arange(0,101,1) 

plist = stats.poisson.pmf(x,mu)

blist1 = stats.binom.pmf(x,20,0.5) 

blist2 = stats.binom.pmf(x,40,0.25) 

blist3 = stats.binom.pmf(x,100,0.1)

plt.plot(x,plist,label=r'poisson $/mu:10$',color='k') 

plt.plot(x,blist1,'-.',label=r'binomial $n:20, p:0.5$',alpha=0.5) 

plt.plot(x,blist2,'-.',label=r'binomial $n:40, p:0.25$',alpha=0.5) 

plt.plot(x,blist3,'-.',label=r'binomial $n:100, p:0.1$',alpha=0.5)

plt.xlim((-1,20)) 

plt.title(r'Poisson and Binomial Distribution') 

plt.grid() 

plt.legend() 

plt.show()

指数分布

我们继续刘姥姥的故事。

话说这刘姥姥还有个孙子刘小笨，随着刘姥姥和刘大耳的买卖日益红火，刘小笨的伙食也越来越好，饱暖思学术，开始成天开始研究算术。刘小笨天天看刘姥姥卖调料，发现卖出一份调料所需要的时间间隔符合某种分布。经过思考，他决定把这种分布称为指数分布。

经过后人对刘小笨的著作进行解读，我们发现了他的思考过程。

这里我们先考虑简单的量，比如卖出一份调料所需要的时间大于1个时辰（2个小时，120分钟）的概率，其实和1个时辰内一份调料也没有卖出的概率，之和为1。

另外，假设每个时辰平均卖出的调料数为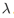（根据刘姥姥的记录，我们知道这个数近似为2）。记随机变量Y为两次卖出调料之间的时间间隔。根据之前刘大耳的假设，立刻有：

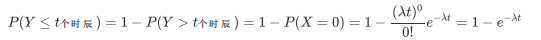
至此，刘小笨可以估算任意时刻他姥姥卖出一份调料的概率。比如，任何1个时辰内，会有调料卖出的概率是：

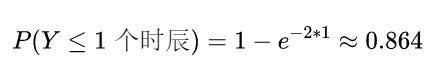
而在接下来的30分钟到60分钟内，会有调料卖出的概率是：

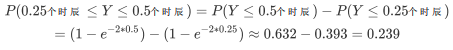
事实上，到这里我们已经得到了图片的累计分布函数了:

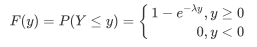
对其求导就可以得到其概率密度函数：

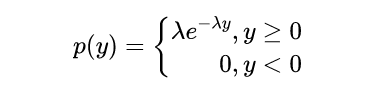
至此，我们就得到了刘姥姥连续两次卖出调料的时间间隔图片的概率密度函数，随机变量就符合指数分布，其中的图片指的是每个时辰平均卖出调料的份数（这里是2） 。

指数分布的图像我们可以画出来，如图3。

import numpy as np 

from scipy import stats 

from matplotlib import pyplot as plt

x = np.arange(0,10,0.1) 

elist1 = stats.expon.pdf(x,scale=1/2) 

elist2 = stats.expon.pdf(x,scale=1/3) 

elist3 = stats.expon.pdf(x,scale=1/5)

plt.plot(x,elist1,label=r'$\lambda:2$') 

plt.plot(x,elist2,label=r'$\lambda:3$') 

plt.plot(x,elist3,label=r'$\lambda:5$') 

plt.xlim((0,3)) 

plt.grid() 

plt.legend() 

plt.title(r'Exponential Distribution PDF') 

plt.show()

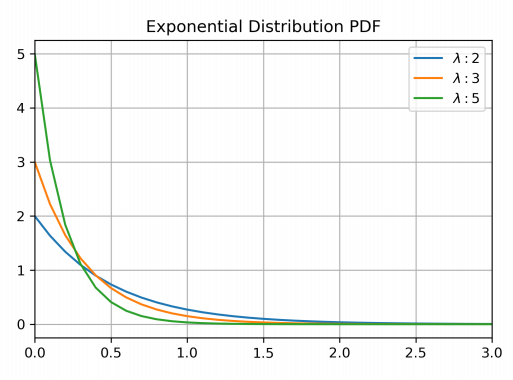
可以从图中看出，当每个时辰卖出更多的调料份数时，更小的连续两次卖出调料时间间隔发生的概率更高，这很合理。

用一句话来概括，每天卖出的调料份数服从的是泊松分布，而卖出两份调料的时间间隔服从指数分布，它们的期望分别代表了平均每天卖出的调料份数和每份调料卖出的平均时间间隔。真实世界中同样有很多场景也和指数分布有关，比如某网站被访问的时间间隔；客服中心连续接到电话中间的休息时间间隔；电子产品的寿命（出现故障的时间间隔即正常使用寿命）……

伽马分布

我们紧接上面的故事展开后续。

话说刘姥姥去世之后，刘小笨和王县令合作开店。这个时候生意更好了，王县令粗略统计了一下，发现平均每个时辰能卖出100份调料。他于是问刘小笨：昨天刚做好的那300份调料都卖光的时间满足什么概率分布？刘小笨沉吟片刻，感觉这种分布和之前的泊松分布指数分布都不一样，于是他把这种分布称作：伽马分布。

刘小笨后来的手札记录了他当时的思考过程。

假设每份调料卖出都是相互独立的，而单位时间卖出调料份数均值为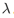。则在这里，从开张到卖出到当日第X份调料所需要的时间随机变量T_x(t)就是我们应该关注的量。我们假设该随机变量分布的概率密度函数为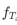。进一步的，我们根据概率密度函数定义有：

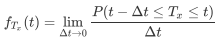
而我们同样可以使用处理泊松分布时的方法，将t均分为k份，计算当k趋近于无穷大时的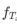。需要注意的是，t时间后，我们应该卖出了第x份，也就是说，在将t这一时间段分为k份后，前k-1份中我们肯定已经卖出了x-1份调料。假设每一小份时间段内我们卖出调料的概率为p，那么这么问题又退化成了二项分布相关的问题。

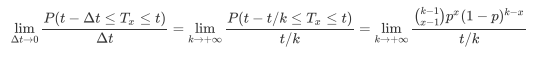
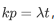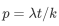根据期望的定义，我们有， 将带入上式。

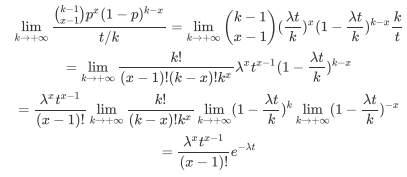
至此，我们得到了伽马分布的概率密度函数。更一般，当我们允许X为小数时，可以对阶乘做适当的解析延拓，也就是伽马函数了。

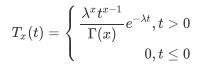
别看这式子如此复杂，实际上伽马分布就是要解决计算从此时到后X次随机事件都发生，需要等多长时间的问题。

显然，当x=1时，退化为了指数分布，即要解决的问题退化为了计算下一次发生该随机事件的时间间隔问题。

我们来看看伽马分布密度函数的函数图像。

import numpy as np 

from scipy import stats 

from matplotlib import pyplot as plt

x = np.arange(0,10,0.1)

glist1 = stats.gamma.pdf(x,1) 

glist2 = stats.gamma.pdf(x,2) 

glist3 = stats.gamma.pdf(x,3)

plt.plot(x,glist1,label=r'$x:1$') 

plt.plot(x,glist2,label=r'$x:2$') 

plt.plot(x,glist3,label=r'$x:3$') 

plt.grid() 

plt.legend() 

plt.title(r'Gamma Distribution PDF: $\lambda:1$') 

plt.show()

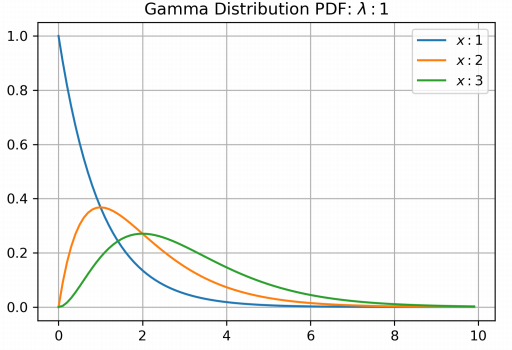
至此，我们讲解完了泊松分布，指数分布和伽马分布。

总结一下，泊松分布解决的是离散事件发生在连续的时间内的次数概率分布的问题；指数分布解决的是独立离散事件发生一次所需连续时间长度分布的问题；伽马分布解决的是多次离散事件发生所需连续时间长度分布的问题。其中，指数分布是伽马分布的特例。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。