介绍

与纯频率论方法相比，贝叶斯分析提供了从数据中获得更多见解的可能性。本文将通过一个真实的示例向您介绍如何使用贝叶斯分析。本文将演示选择错误的先验时可能出问题的地方，并且展示如何总结我们的结果。为了让您理解这篇文章，我假设您已经熟悉贝叶斯统计的基础和贝叶斯定理。

情境

作为示例分析，我们将讨论物理实验室中的真实问题。不用担心，您不需要任何物理知识。问题的目标是确定粒子探测器的效率。粒子检测器是一种传感器，当某些粒子经过时会产生可测量的信号。检测器效率是检测器实际测量到横越粒子的机率。为了对此进行测量，我们将要评估的检测器放在其他两个传感器之间，呈三明治状。如果我们在顶部和底部传感器中测量信号，我们知道粒子也应该在中间穿过检测器。实验设置的图片如下所示。

我们要测量粒子检测器（被测设备）的效率。在检测器的顶部和下方放置了两个不同的传感器（触发器），以检测穿过设置的颗粒（在本例中为μ）

需要被测量的数据为在一定时间内（由顶部和底部传感器报告的）通过的粒子的数量N，以及在探测器中测得的信号数量r。对于此示例，我们假设N = 100和r = 98。

频率论结果

使用频率论方法，我们可以直接通过测量数据得出结论，即探测器的效率为e = r / N = 98％。但这仅算出了一个点估计（point estimation）。如果我们要回答更复杂的问题，例如：“检测器的效率高于99％的概率是多少”，那么我们需要进行更复杂的分析。

贝叶斯分析

贝叶斯方法的作用是在给定数据p（e | D）的情况下，得出探测器效率的全部后验概率分布。为此，我们需要使用贝叶斯定理：

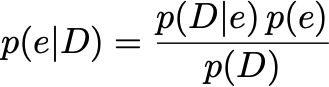
Bayes'Theorem

下面我们将讨论不同的术语。

概率模型/可能性：p（D | e）

使用贝叶斯分析时，我们需要选择一个模型来描述我们要分析的过程，即可能性。对于先前提到的探测器问题，我们可以将效率解释为在一定数量的线索（N）中获得成功（r）的机会。此类问题类似于确定硬币出现正面的机会，可以通过二项分布来建模：

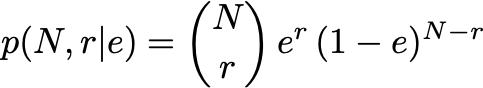
Binomial Distribution

先验：p（e）

接下来，我们需要定义一个先验。在这里，我们从最简单的选择开始，即扁平先验（flat prior）。稍后，我们将讨论选择不同先验的影响。

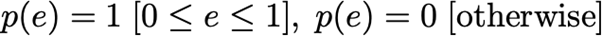
边际可能性：p（D）

边际可能性是贝叶斯定理中的分母。幸运的是，它只是一个归一化常数，与效率无关。我们可以通过找到将后验归一化为1的常数来确定它的数值。

结果

现在我们可以通过贝叶斯定理来计算后验。

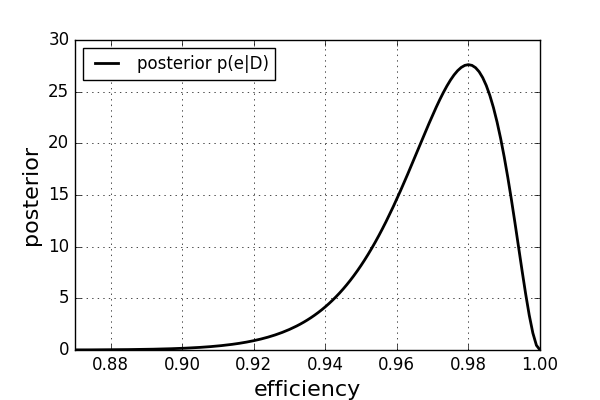
N = 100，r = 98，后验分布p（e | D）

您可以看到最可能的值是e = 98％，这与直观的频率论的结果相同。但是，由于获得了完整的后验概率分布，我们在这里获得了更多的信息。例如，我们可以看到分布是不对称的。低于97％的效率比高于99％的效率更高。对于这两种概率，我们可以分配确切的数字。我们如何获得这些额外信息？这是因为我们利用了更多的信息，这意味着我们假设检测器的行为遵循二项式分布，并且假设了先验分布平坦。

先验的影响

先验在贝叶斯分析中起重要作用。在下面，我们将看到如果更改它会发生什么。假设我们在检测器的数据表中找到一条陈述，即效率可以假定为（中心）在98%附近且标准偏差为1%的高斯分布。但是，在较早版本的数据表中，我们发现检测器的效率应为（中心）在92%附近，标准偏差也为1%的高斯分布 我们通过相应地更改先验将这些信息合并到后验中。这两种情况的结果都可以在下面看到。

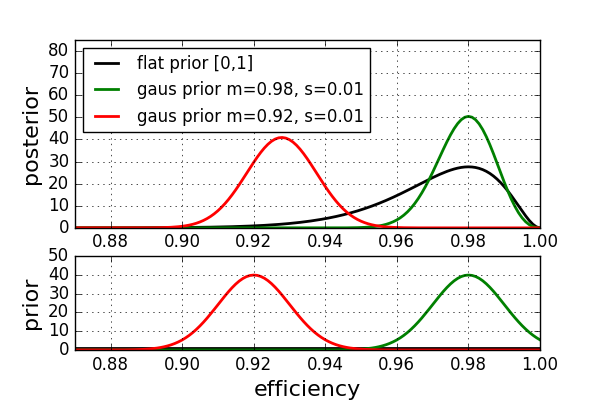
不同先验的后验概率和先验概率

在这里，后验显示在顶部面板中，而相应的先验显示在下方面板中。黑色曲线显示先前平坦先验的结果。当将先验转换为均值m = 98％（绿色）的高斯验算器时，后验峰再次出现在98％，并且与持平先验者相比，我们的估计信心更大。先验支持我们的数据。尽管对于之前的单位而言，效率低于95％仍然有合理的可能性，但现在几乎将其排除在外。从旧数据表中的先验数据以92％（红色）的效率达到峰值，我们可以看到，后验数据与其他两个数据表明显不同。最可能的值约为93％，这完全改变了我们的结果。怎么会这样？问题在于选择了与数据不一致的错误先验。此示例表明，选择错误的先验可能会带来灾难性的后果。评估先验、概率模型和后验之间的一致性是很重要的。

合并其他度量

先验的另一个用例是额外的度量。想象一下您的同事测量了相同的检测器。他测得N1 = 300，r1 = 280。我们如何正确利用这些数据？我们可以将其用作分析的先验条件。结果如下所示。

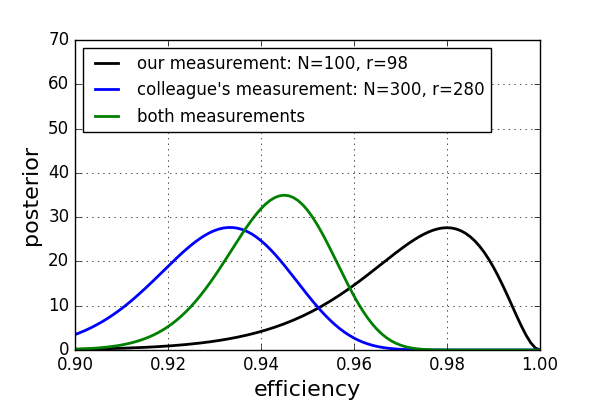
使用先前的测量作为先验

您可以使用平坦先验值来查看我们的度量的后验分布（黑色）和同事的度量（蓝色）。如果我们将同事的测量结果作为分析的先验条件，则会得出绿色曲线。绿色曲线的最可能值在其他两条曲线之间，但是随着我们同事的测量结果具有更多数据，更多地转移到了蓝色曲线。此外，绿色曲线的分布比其他两条曲线略窄。

旁注：产生的后验依旧是二项分布。此外，我们将得出相同的后验，就好像我们要重做分析一样，并假设仅使用N = N1 + N2 = 400和r = r1 + r2 = 378进行一次测量。如您所料，结果也与两次测量的执行顺序无关。可以很容易地进行分析验证。

如何呈现结果

在计算后验后，我们现在要介绍我们的结果。理想情况下，您希望显示完整的后验分布，因为这反映了完整的信息。但是，这并非总是可能的，您可能需要用一组值对其进行总结。通常，您需要给出一个点估计值以及一个总结分布宽度的间隔。有多种方法可以做到这一点。热门选择包括：

• 期望值和标准差

• 中位数和中心区间

• 众数和最小区间

此外，我们需要选择在区间中应包含多少概率（通常使用：68％或90％）。

对于正态分布，点估计和置信区间的所有三个选择都给出相同的结果。但是，在我们的分布偏斜的情况下，情况并非如此。

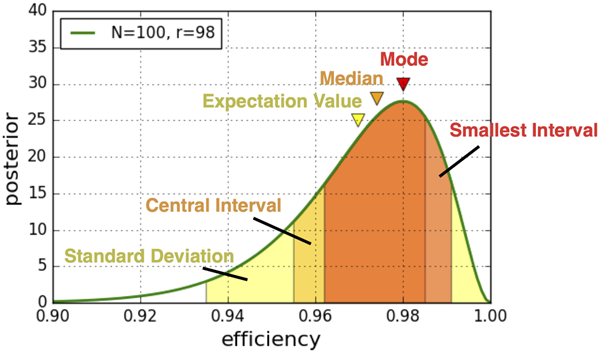
点估计和相应区间的不同组合，以便总结后验

您会看到所有三个选择导致不同的结果。这些都不是错误或正确的，重要的是准确报告您使用的点估计以及区间的构造方式。在这里我们可以说，例如，我们后验的最可能值（众数）为0.98，置信区间为0.962-0.991（最小区间，包括68％的概率密度）。

结论

我们通过先建立概率模型、选择合适的先验条件，直到最后用一个点估计和相应区间总结后验概率来演示了完整的贝叶斯分析。贝叶斯方法的优点是我们可以访问全部后验概率分布。这使我们能够优雅地合并先前的知识，例如制造商的信息或先前的度量。此外，我们发现错误的先验的选择可能会对我们的结果产生重大影响，这强调在任何贝叶斯分析中，谨慎选择先验并评估其与概率模型和后验的一致性都是非常重要的。

原文链接：

https://towardsdatascience.com/performing-a-bayesian-analysis-by-hand-c589ab992916

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。