目标

本小节将寻求以下问题的答案：

什么是傅立叶变换，为什么要使用傅立叶变换？

如何在OpenCV中使用傅立叶变换？

 copyMakeBorder() , merge() , dft() , getOptimalDFTSize() , log() 和 normalize() 等函数的使用方法。

源代码

可以到

samples/cpp/tutorial_code/core/discrete_fourier_transform/discrete_fourier_transform.cpp目录下查看OpenCV的源代码库。

下面是dft（）的应用示例程序：

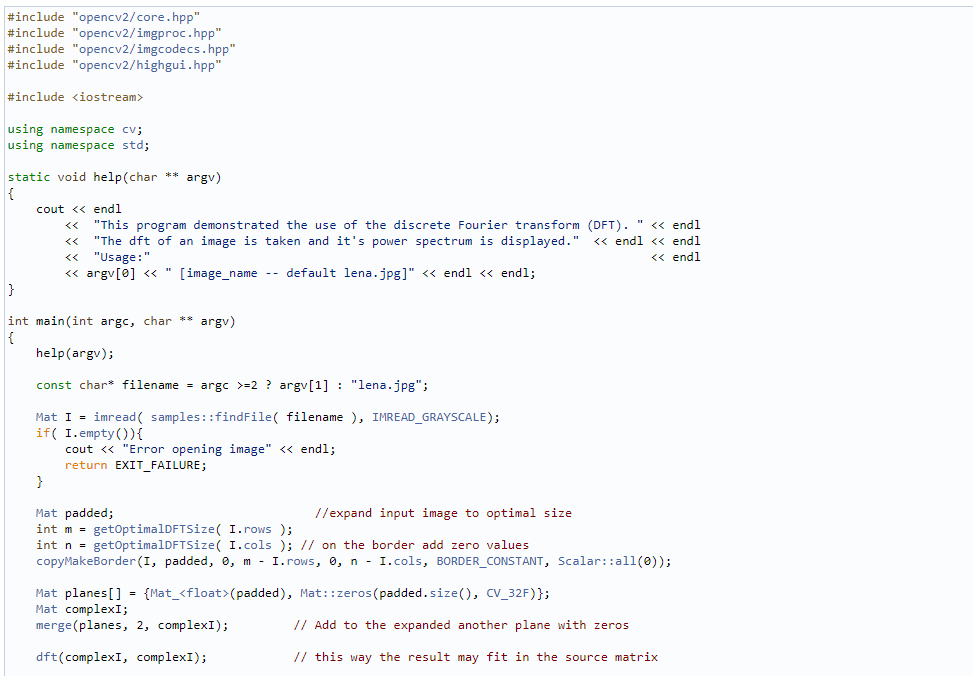
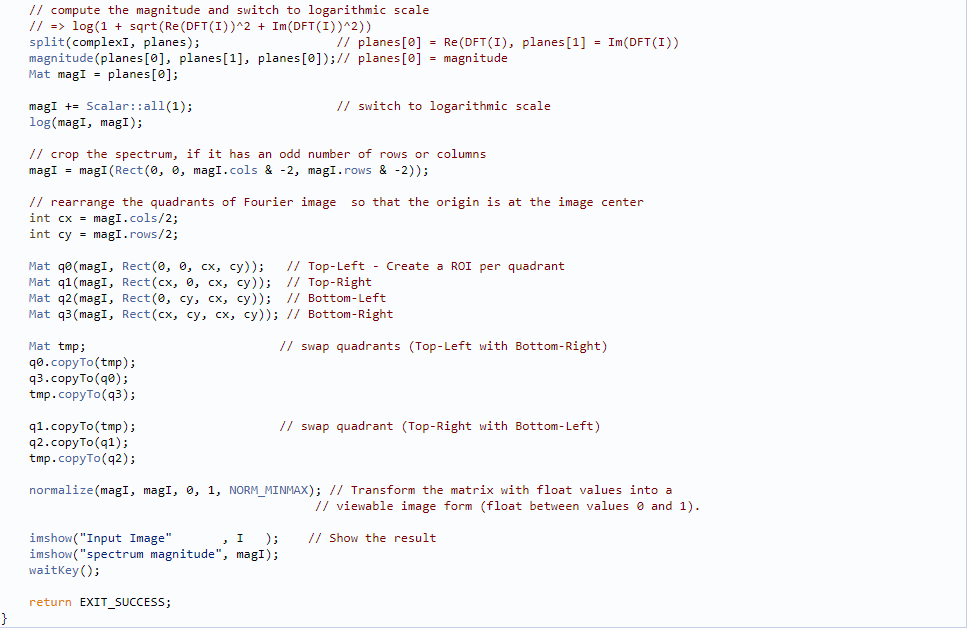
代码详解

傅立叶变换可以将图像分解成正弦和余弦分量。也就是说，它将图像从空间域变换到频率域。其主要思想为：任何函数均可以用无限多个正弦和余弦函数之和来精确近似。傅立叶变换正是这一想法的实现。数学上，一张二维图像的傅里叶变换可表示如下：

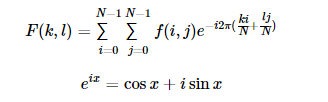
这里，f是图像在空间域的图像值， F是图像在频率域的图像值，转换后的结果为复数，可以通过并且可以用实数图和复数图进行表示，也可以用幅度和相位图进行表示。然而，对于图像处理算法而言算法仅关注图像的幅度信息，因为其中包含了图像几何结构中的所有信息。如果想通过对复数图像或幅度/相位图像下的象函数进行修改，从而间接地调整原函数， 那么则需要保留象函数的值，并进行傅里叶变换逆变换，从而获得调整后的原函数的数值。

在此示例中，将介绍如何计算和显示图像经过傅里叶变换的幅度图值。假设数字图像的傅里叶变换是离散的傅里叶变换，可以在给定的域值中任取一个数值。例如，灰度图像的像素值通常在0到255之间，那么傅立叶变换的结果也是离散型的。当需要从几何视角来确定图像的结构时，便可适用DFT。下面是离散型的傅里叶变换（DFT ）的实现步骤（假设输入图像为灰度图像I）：

将图像展开到最佳尺寸

DFT的性能取决于图像的大小，当图像的尺寸为2，3，5 的倍数时，离散傅里叶变换（DFT ）的速度最快。因此，为获得最优的性能，可以通过调整图像的边界值来获得便于快速计算的图像尺寸。getOptimalDFTSize（）函数返回一个最优尺寸的图像，使用copyMakeBorder（）函数扩展图像（将增加的像素值初始化为零）的边界：

为复数的实部和虚部开辟存储空间

傅立叶变换的结果是复数，这意味着，每个图像对应着两个像素值（实部和虚部各一个分量）。此外，频率域范围比其对应的空间域范围要大得多，所以至少要用浮点（float format）的格式来存储傅里叶变换的结果。为此，需要将输入的图像数据类型转换成浮点类型，并扩展出另一个通道来保存复数值：

离散傅立叶变换

进行原位计算（输入数据同输出数据）：

将复数的实部和虚部转换成幅度值

复数包含实部(Re)和虚部( Im) 两部分。DFT的结果为复数，这个复数的幅度为：

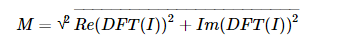
转换成OpenCV的代码如下：

切换到对数尺寸

由于傅里叶系数的动态范围过大，无法在屏幕上显示，

一些较小和较大的变化值也无法在线性尺度下观察到。因此，较高的数值会变成白点，而较小的数值变为黑点。为了便于显示全部数值，可使用灰度值，并将线性尺寸变换成对数尺寸：

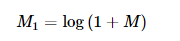
转换成OpenCV代码如下：

剪裁和重排

在上述第一步中，对图像的尺寸进行了扩展，在这里则需要抛弃由图像扩展而新引进的像素值。为了方便可视化，对结果值的象限重新排列，使得原点（零，零）对应图像中心。

归一化

归一化的目的也是为了便于可视化。经过运算之后，获得了幅度值，但这些数值仍然超出了图像的显示范围（从零到一），为此，利用cv::normalize()函数对幅度值进行归一化，取值在零到一的范围之内。

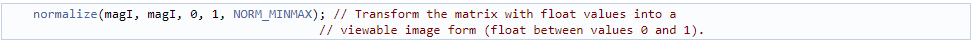
结果

应用傅里叶变换的主要目的是要确定图像的几何方向。例如，如何看出文本是水平还是垂直方向的？对于某些文字来说，文本行的排序形式是水平线，而字母则形成某种垂直线。经傅里叶变换后，仍然可以看到文本中片段中的两个主要部分。下面，分别用水平和旋转图像来描述某一文本。

水平文本图像：

旋转文本图像：

从中可以看出，频域中影响最大的分量（幅度图像上最亮的点）会随着图像的几何位置旋转，可以根据这一点计算出偏移量，通过旋转图像来对位置进行纠正。

注：本文以C++语言代码为例，获取Java和python版本可在原文中查看：

https://docs.opencv.org/4.5.2/d8/d01/tutorial_discrete_fourier_transform.html

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。