作者 : Georgi Georgiev

翻译：Gabriel Ng

校对：张玲

从115个公开的A/B测试中你能够得到什么信息？通常情况下并不会太多，原因在于大部分情况下，你只能看到有关被测对象的基本数据和A/B测试结果。另一方面，置信区间、p值以及其他针对不确定性的度量则往往被遗忘，而即使有，它们的计算也不尽人意，又或者背后的统计过程没有分享出来，使得它们实际上难以使用。一个数据来源︰GoodUI.org有稍微好一点的方法，在他们网站上发布的每一个测试都附上了基本的统计信息︰用户数量、每个测试变量的转换以及被试对象是什么。

笔者决定收集这些数据，并对这115个测试（在下文展示）进行统计上的元分析。除了对A/B测试或转换率优化活动的样本的平均结果作出总结以外，这样做更多的是为了在设计和分析A/B测试时，能作为一个更好的统计习惯的指引。

一个主要发现是相对于预期的结果和成本经济逻辑，大约70%的测试有着低下的检定力，暗示着有自选停止的问题。经过数据修剪和统计上的调整后，余下的85个测试显示出4%以下的平均值和中位数相对提升，当中统计显著的平均值为6.78%，中位数为5.96%。

因为GoodUI这个样本并不能代表所有完成的A/B测试，所以对于整个A/B测试流程的任何形式的一般化都应该谨慎处理。

笔者首先会讨论初始数据必要的修剪，然后分享元分析的详细结果，最后作出一个简短的总结。

统计意义上的重新计算和数据修剪

GoodUI上的数据有对统计显著度的计算和置信区间，同时也有结果的自评︰"不显著"、"有可能"、"显著"、"强"，两个方向都有。数据也包含了所观察到的百分比改变。因为有报告的样本大小，也能对检定力作出计算。

以百分比变化形式展示，整个数据集的观察效应估计分布如下︰

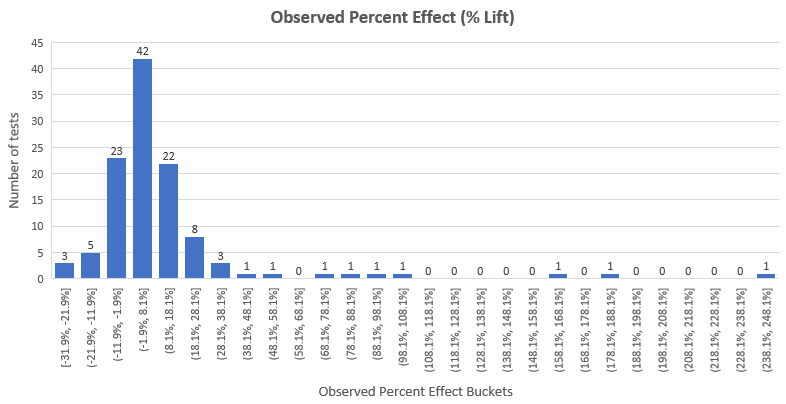
我们可以看到，结果几乎服从正态分布，效应提升的平均值在12.33%，除了右边有重尾分布。这个问题我们在下面的文章会展开讨论。效应提升的中位数是4.89%，代表着在50%的测试中观测到的效应提升小于4.89%，而真实的效应提升可能更小。注意这里也包含了那些没有通过95%显著性检验的测试的观察效应提升。

统计显著度和置信区间的重新计算

很不幸的是，在人工提取每个测试的用户数目和转换后，笔者需要优先重新计算统计显著度(p值)和置信区间的上下限，原因是网站上的统计信息有两个问题︰

1. 显著度和置信区间的计算都是以双边对立假设，而非单边对立假设作为基本，而在进行方向性的推断时，显然单边对立假设更合理。

2. p值(统计显著度)和置信区间是为了计算绝对差异，但推断目标却是百分比改变（百分比提升）。因此，笔者用了恰当的p值和置信区间来表示百分比提升。

第一个重新计算有着较预期少的不确定性，而第二个重新计算则有着较预期高的不确定性。整体上，相较原来的显著性水平和置信区间，重新计算使得不确定性减少，原因在于单边对立假设的修正抹除了百分比提升的改正。

我们可以看到，115个测试中有18个测试结果重新评级︰

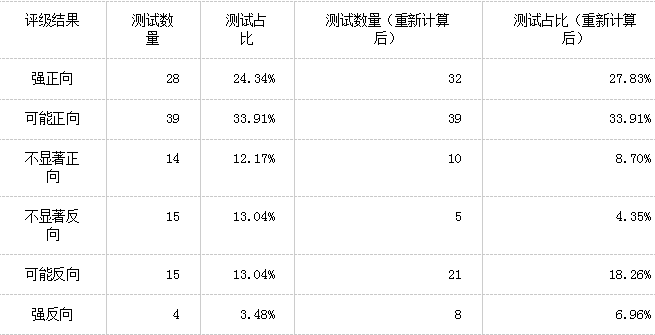
根据GoodUI的定义，有︰

p值小于等于0.03为强结果，p值小于等于0.25为可能结果，p值大于0.25为不显著结果。每一个评级结果都是连续的（例如若果p值为0.01，则测试的评级不能同时为强和可能）。GoodUI也定义了每个评级所需要的样本大小，但这是不合理的，因为p值的恰当计算包括了样本大小的调整，这比GoodUI粗略的做法来得好。

按照更为经典的p值阈值︰0.05（95%置信度），我们获得了45个统计上显著的成功结果和12个统计上显著的失败结果（分别为整体测试的39.13%和10.43%），余下的58个测试（50.44%）则有着不显著的结果。恰当p值的分布如下︰

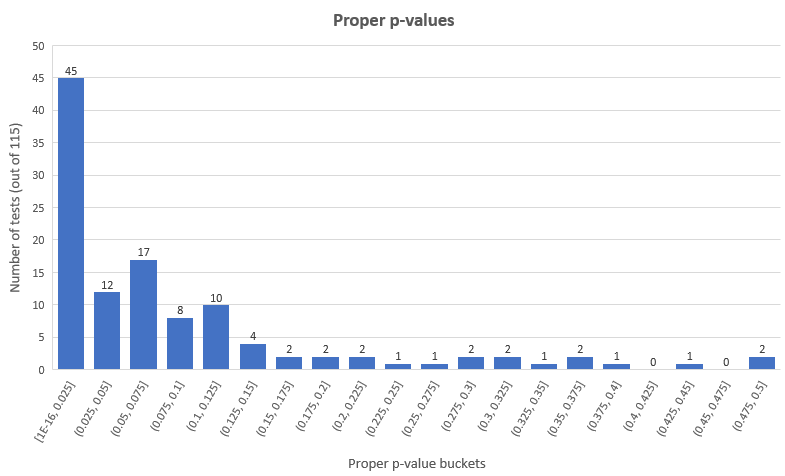
这是p值在0.05以下的测试的观测效应，恰当计算后，提升效应百分比的单尾p值如下：

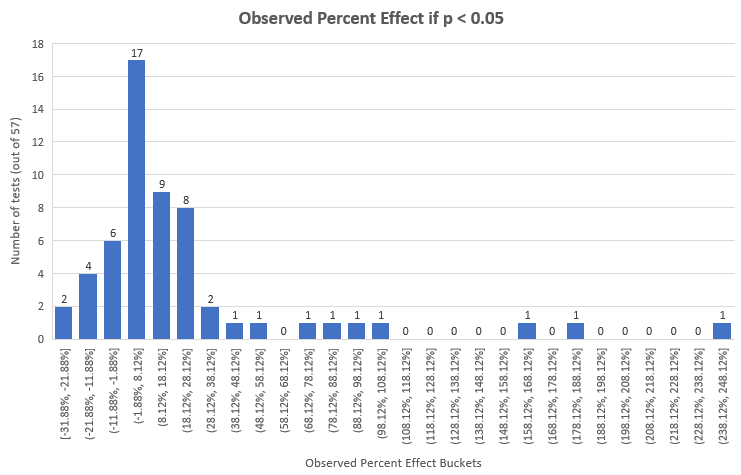
当然，比起整体，这些测试有着较高的平均值和中位数︰22.94%和7.91%，但它们只占115个中的57个。

不平衡测试的移除

115个的测试中的3个（#55，#72，#90）在对照组和实验组的用户数目上有着显著的不平衡。在第一个情景中，相较于对照组（样本大小为每组200,000+），实验组有着16%更多的用户数，而在其后的两个情景中，分别为9%和13%更少的用户数（样本大小为20,000+和10,000+）。我们可以猜测以下原因︰不恰当的随机化、技术问题引致一部分用户没有体验整体实验、采用了如多臂老虎机或在测试期间重新平衡臂的类似方法等等。

唯一合理的解释是随机化过程中，实验组和对照组流量分配不均，数量如此之多，以至于笔者怀疑就是这么回事。

如果原因是以上任何一种不合理的解释，那么很明显地任何以这一数据为基本的统计分析都会是带有偏差的。由于出现了妥协性随机化，并且笔者高度怀疑有意的不均等分布，笔者决定在最后的分析中移除以上3个测试。

明显妥协性测试的移除

在对A/B测试进行统计设计和分析时，一个常见的问题是在没有任何统计上的调整下，多次地重复窥探数据，以获得所需要和希望的数据。这种方法一般被称为︰”显著度等待”。

只需几次观察就能大大地提高显著(名义上的)结果的似然性好几倍，即使真实的观察可能性非常低。举个例子，一个有着实际上0.08p值的测试，在经过5次窥探后，就可以得到一个名义上的0.025 p值，这里实际上的p值大大偏离了0.05阈值，且是名义上的p值的3.2倍。现在我们有多种方法去观察收集数据，而其中一种是”敏捷A/B测试方法”。

发现妥协性测试的一种方法是寻找检定力低得不切实际的测试。我们可以通过询问自己以下问题来达到这一效果︰如果我正在设计测试时，考虑到干预的规模、 X%真实提升的预期效益、固定成本、可变成本等等，我会对什么样的功效水平感到满意（在文章Risk vs. Reward in A/B Tests: A/B testing as Risk Management一文中有详细介绍怎样选择合适的样本大小检定力和显著性水平）。

举例说，没有人会在变量只有轻微改变（例如按钮的内容文字）的情况下，去设计一个有着90%检定力，去侦测20%相对变化的测试。在这种情况下，去预期干预有着巨大程度的结果是不现实的，也会因为测试的检定力低下而白白浪费测试资源。所以当人们在决定合理样本大小和最小可检测效应时，一个应该自问的问题是︰怎么样的结果是令我们鼓舞的？是1%，2%，5%，还是20%？问题的答案因测试而异，但在A/B测试中很少会高于10%。

因为上述原因，合理的设计者不会在大于40%的最小可检测效应（Minimum detectable effect, MDE）情况下，设计有着90%检定力的A/B测试，原因是这会使得侦测任何低于MDE的真实效应的机会变得非常低。这一点从熟悉的”效应大小/检定力函数”的图像中就能看到。

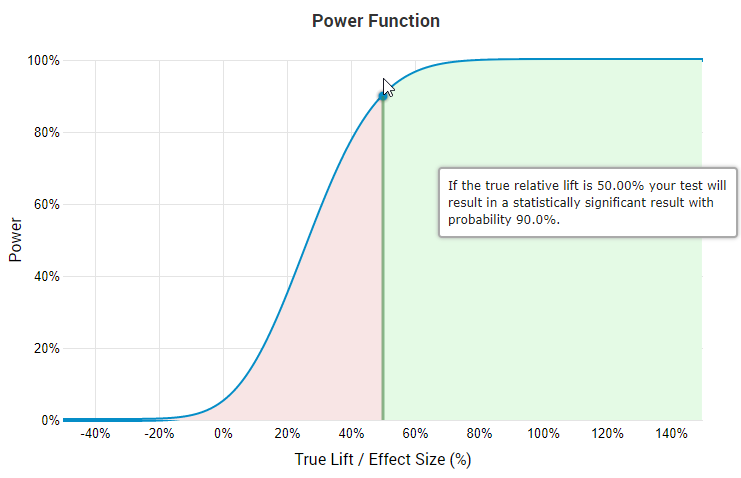
如果真实相对提升为50%，那么根据图像，测试会有90%的机会有着显著结果。

上图来源是A/B测试统计计算器，在图中能看到如果要以90%检定力去侦测50%的真实提升，那么只有45.7%的可能性侦测到25%的真实提升，且对于越小的真实效应，其可能性也越小。笔者并不对在这些水平下仍经济上合理的测试感兴趣。而且对于大部分测试，即使是在数据修剪前效应大小的中位数也有着4%-5%。这进一步说明在显著高的水平下设计有着最小可检测效应的测试是不合理的。

所以如果我们希望在115个测试中侦测出妥协性测试，在90%检定力下，观测测试效应大小的分布是一个值得的举动。下图是实际结果（平均最小可检测提升是27.8%，中位数是20.84%）︰

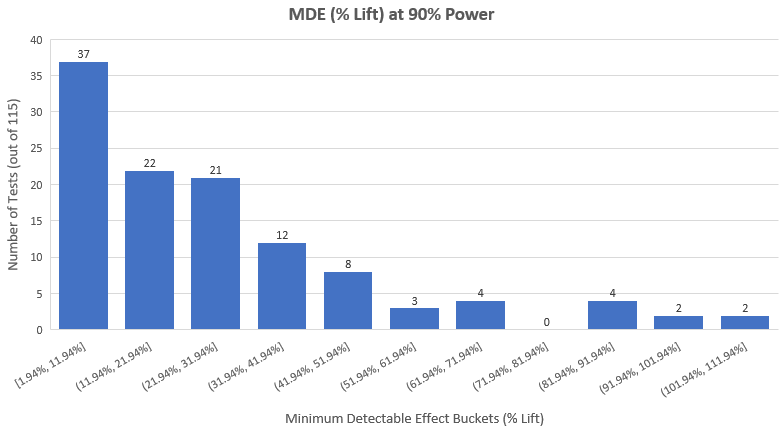
第一眼就明显的情况是︰

1. 有一大堆测试，它们的设计者认为测试有天文级别的改善效果。

2. 有一大堆测试，只有在天文级别高的结果下才经济合算。

3. 有一大堆人在没有固定样本大小的前提下进行测试，而且常常窥探数据，最后若无其事地分析结果。

笔者认为情况3最有机会代表大部分的测试。即使没有像情况3那样做，他们也是用了某种恰当的相继性分析。正确的测试是这样的︰p值的计算吻合固定样本大小测试的计算结果，而且它们只有在固定样本大小的测试下才变得合理。

通过对每一个测试的干预进行人工检视，结合笔者对于在这些干预中的合理效应大小的知识，以及A/B测试的经济效益。笔者得出了自己（某程度上的主观）的评估结果，在115个测试中的80个（69.57%）是低检定力的，从而笔者怀疑当中有不同程度的自选停止。这里，笔者必须指出其假设已经是相当宽松的。

虽然如此，笔者仍无意为了阐释评估结果中的主观部分，而单单对30个测试作出分析，故笔者决定只移除最为明显的出错例子︰在90%检定力和0.05（95%信赖度）显著水平的情况下，有着最小可检测提升为大于等于40%的测试。注意，笔者在检定力的计算中已是十分宽松，因为在GoodUI的分类中，p值的阈值为0.03，而不是0.05。

数据修剪的结果是，有25个测试被移除，因未解释的自选停止（数据窥探）下而出现了明显的妥协行为。因为没有关于窥探次数和时间的信息，我们没有办法去对p值和信赖区间作出调整以抵偿数据的窥探。被移除的总测试数变成28（当中3个是因为不平衡的样本大小），可供分析的测试有87个。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。